Binary Search
Summary
2024年9月9日更新:不要想那么多的模板,记住区间的开合关系即可,比如用左闭右开区间 [), 和 python 很像,则代码有几个注意点:
- left = 0, right = len(nums); 因为 right 取不到
- case 1: nums[mid] < target: left target mid right: 此时需要更新 right = mid, 因为取不到,不需要 mid - 1
- case 2: nums[mid] > target: left mid target right: 此时需要更新 left = mid + 1 不要重复取值
参考 B 站:代码随想录,很清晰。
1. 二分搜索模板
1.1 基本的二分搜索算法
手工实现
class Solution: def search(self, nums: List[int], target: int) -> int: if not nums: return -1 l, r = 0, len(nums) - 1 while l <= r: mid = l + (r - l) // 2 if nums[mid] < target: l = mid + 1 elif nums[mid] > target: r = mid - 1 else: return mid return -1使用 Python
bisect库def search_2(self, nums: List[int], target: int) -> int: res = bisect.bisect_left(nums, target) if res != len(nums) and nums[res] == target: return res return -1
1.2 寻找左侧边界的二分搜索
手工实现
def search(self, nums: List[int], target: int) -> int: l, r = 0, len(nums) - 1 while l <= r: mid = l + (r - l) // 2 if nums[mid] < target: l = mid + 1 elif nums[mid] > target: r = mid - 1 elif nums[mid] == target: # 暂时不能返回,需要收缩右边界,锁定左侧边界 r = mid - 1 # 检查越界情况。注意这边下面两个条件是二选一的 if l >= len(nums) or nums[l] != target: return -1 return l使用
bisect手工实现在很多情况下都需要调试,比较慢,因此使用
bisect比较方便,其使用方式如下:找到 Find rightmost value less than target:找到小于目标元素,离目标元素最近的元素(肯定在左边)。如
[-1, 1, 3, 5, 9, 12]目标元素 2, 则返回了 1,表示 2 可以插入到 1 和 3 之间。对应的下标res - 1就是 1 的下标。def search2(self, nums: List[int], target: int) -> int: res = bisect.bisect_left(nums, target) if res: return nums[res - 1] return -1找到 Find rightmost value less than or equal to target
def search3(self, nums: List[int], target: int) -> int: res = bisect.bisect_right(nums, target) if res: return nums[res - 1] return -1
1.3 寻找右侧边界的二分搜索
手工实现
def search(self, nums: List[int], target: int) -> int: l, r = 0, len(nums) - 1 while l <= r: mid = l + (r - l) // 2 if nums[mid] < target: l = mid + 1 elif nums[mid] > target: r = mid - 1 elif nums[mid] == target: # 暂时不能返回,需要收缩左边界,锁定右侧边界 l = mid + 1 # 检查越界情况。注意这边下面两个条件是二选一的 if r < 0 or nums[l] != target: return -1 return r使用库
def find_gt(a, x): 'Find leftmost value greater than x' i = bisect_right(a, x) if i != len(a): return a[i] raise ValueError def find_ge(a, x): 'Find leftmost item greater than or equal to x' i = bisect_left(a, x) if i != len(a): return a[i] raise ValueError
1.3 参考
在二分查找中,要特别注意边界的问题,二分查找的边界,分为 [left, right) 和 [left, right].
- 初始化时,形式为
left = 0, right = n, 其中n表示数组的长度,由于数组取不到下标n, 故为左闭右开区间; - 初始化时,形式为
left = 0, right = n - 1, 故为左闭右闭区间。
bug!!!
对于左闭右开区间([left, right) )而言,应注意:
在写代码时,应当注意边界条件:
如果初始化为左闭右开区间,则当 mid 的值小于要查找的值的时候,left = mid + 1 是正确的
而当 mid 的值大于要查找的值的时候(这时候需要向左查找),此时如果让 right 赋值为 mid - 1, 则有可能存在 mid - 1 正好是要查找的值的情况,要十分慎重。
基于此,在写二分查找时,可以基于以下原则:标准程序参考链接
- 使用左右闭区间初始化,查找后条件应当变成:
left = mid + 1andright = mid -1, 否则会出现死循环; - 使用左闭右开区间初始化,查找后条件应当是:
left = mid + 1andright = mid; left初值为-1, 循环条件使用while(left + 1 != right);- 对边界条件专门进行判断。
二分查找思路整理
有下面的例子,可以分为四种问题,提出二分查找:
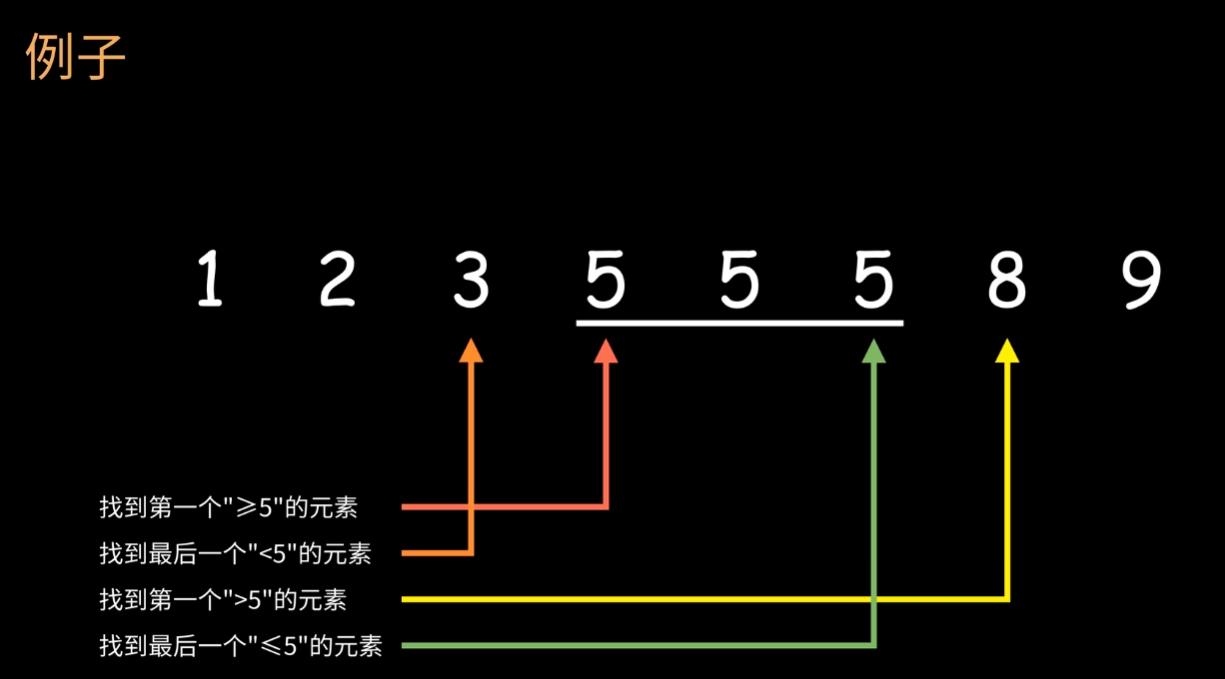
从一个新的角度区理解这个问题,该问题可以变为:找出图中的蓝红边界,即求出未知数K。

针对此问题,可以写出伪代码如下所示:
l = -1, r = N
while l + 1 != r
m = (l + r) / 2 取下界
if isBlue(m)
l = m
else
r = m
return l or r有了以上的伪代码,图1 中的问题答案分别为:
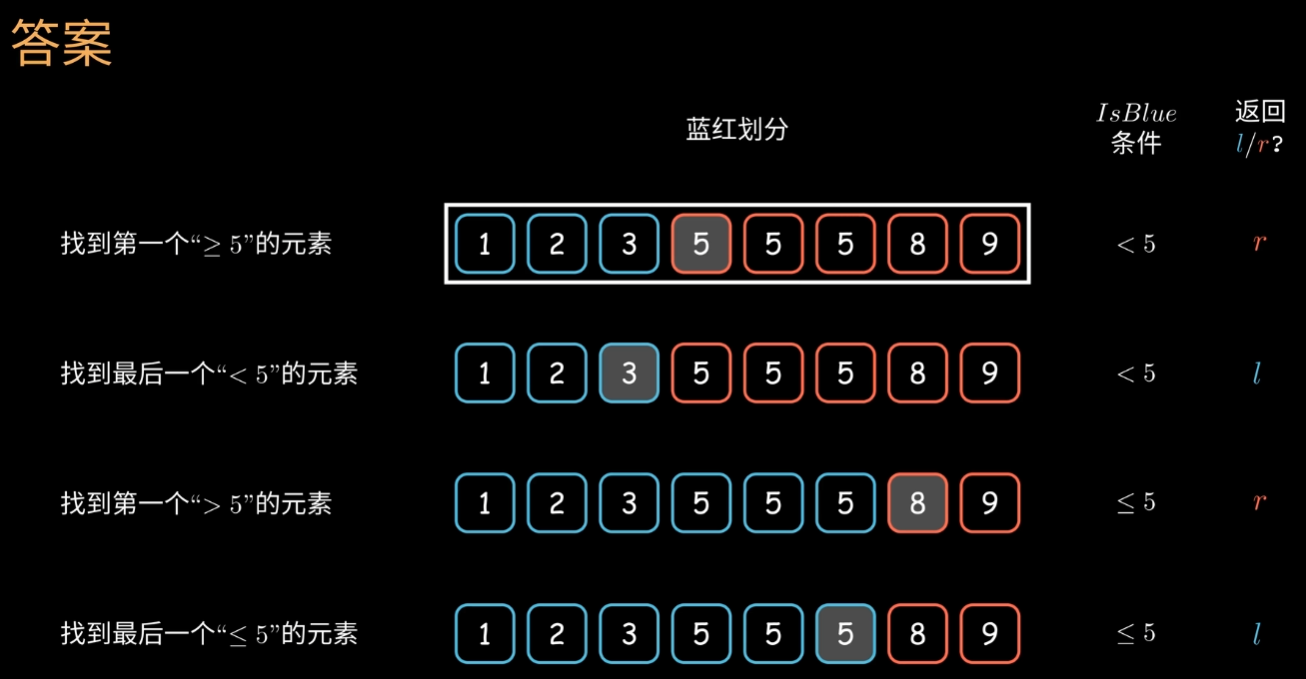
参考视频:https://www.bilibili.com/video/BV1d54y1q7k7
Code
wiki 伪代码
记住口诀
mid 在前,先小后大,先左后右
解析:mid 总是在比较的左边:mid < target; 先写 mid 小于,对应左边 l = mid + 1; 再写 mid 大于,对应右边。
function binary_search(A, n, T):
L := 0
R := n − 1
while L <= R:
m := floor((L + R) / 2)
if A[m] < T:
L := m + 1
else if A[m] > T:
R := m - 1
else:
return m
return unsuccessful查找插入位置
二分查找有序序列中某个元素的位置,如果没找到,则返回其需要插入的位置(LC 035):
def binarySearch(nums, target):
l, r = 0, len(nums) - 1
while l <= r:
mid = (l + r) // 2
if nums[mid] < target:
l = mid + 1
else:
r = mid - 1
return lbisect
或者使用 Python 自带的 bisect:
import bisect
nums = [1, 3, 4, 4, 6, 7]
print(bisect.bisect(nums, 4))
print(bisect.bisect_left(nums, 4))注意到,bisect() 默认会查找元素需要插入的位置,如果是重复的元素,则会返回其最右侧可以插入的位置,使用 bisect_left() 可以返回其左侧位置。
向上、下取整
使用 计算
使用
math.ceil()和math.floor():
imprt math
math.ceil(7/4) # 2
math.floor(7/4) # 1 or 7//4
round(2.6) # 3 四舍五入一般而言,我们在快速排序或者二分查找中如果要计算 mid, 则可以使用 来计算[1]。
Problems
查找二维数组中是否存在某个元素
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。 请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
"""
利用二分查找的思想:
需要遍历每一行得到最后的答案,这个操作顺便复习一下二分查找
"""
def find_in_array_binary_search(self, alist, target) -> bool:
for i in range(len(alist)):
l = 0
r = len(alist[i]) - 1
while l <= r:
mid = (l + r) // 2
# mid = l + (r - l) // 2
if target < alist[i][mid]:
l = mid + 1
elif target > alist[i][mid]:
r = mid - 1
else:
return True
return False提示
注意到这里用到了 先小(<)后大(>), 先左(l)后右 的口诀。
完全平方数
使用二分查找判断某个数是否完全平方数:
def isPerfectSquare(self, num: int) -> bool:
'''
using binary search
'''
l, r = 0, num
while l <= r:
mid = (l + r) // 2
if mid * mid == num:
return True
elif mid * mid < num:
l = mid + 1
else:
r = mid - 1
return False数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数。
使用二分查找,首先查找在前面出现的位置 start, 再查找在后面出现的位置 end, 然后相减得到答案。
这个题目对查找插入位置的概念进行了强化:
class Solution:
def GetNumberOfK(self, data, k):
start = self.get_start(data, k)
end = self.get_end(data, k)
return end - start
def get_start(self, data, k):
l, r = 0, len(data) - 1
while l <= r:
mid = (l + r) // 2
if data[mid] < k:
l = mid + 1
else:
r = mid - 1
return l
def get_end(self, data, k):
l, r = 0, len(data) - 1
while l <= r:
mid = (l + r) // 2
if data[mid] <= k:
l = mid + 1
else:
r = mid - 1
return lFind Peak Element - 寻找峰值
找寻一个数组的峰值
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
这道题目只要求返回一个峰值,所以可以从前往后遍历,遇到符合条件的返回即可,暴力解法和二分法的代码如下:
# 暴力求解
class Solution:
def findPeakElement(self, nums: 'List[int]') -> int:
for i in range(1, len(nums)):
if nums[i] < nums[i-1]:
return i-1
return len(nums)-1
# 二分查找
class SolutionBinarySearch:
def findPeakElement(self, nums: 'List[int]') -> int:
n = len(nums)
if n == 0:
return 0
l = 0
r = len(nums) - 1
while l + 1 < r:
mid = l + (r - l) // 2
if nums[mid] < nums[mid + 1]:
l = mid + 1
else:
r = mid
if l == n - 1 or nums[l] > nums[l + 1]:
return l
else:
return rLC875 爱吃香蕉的珂珂
珂珂喜欢吃香蕉。这里有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K(K 为整数)。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/koko-eating-bananas 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
下面两种解法展示了不同边界条件下该如何处理:
class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
l, r = 1, max(piles)
while l < r:
mid = l + (r - l) // 2
cost = self.check(mid, piles)
# 耗时太多,说明速度太慢了
if cost > h:
l = mid + 1
else:
r = mid
return l
def check(self, mid, piles):
cost = 0
for pile in piles:
if mid >= pile:
cost += 1
else:
# 向上取整
cost += ceil(pile / mid)
# cost += (pile + mid - 1) // mid
return costclass Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
l, r = 1, max(piles)
while l <= r:
mid = l + (r - l) // 2
cost = self.check(mid, piles)
if cost > h:
l = mid + 1
else:
r = mid - 1
return l上述代码的两种解法都是可以的,区别在于边界条件的不同,可以参考比较,加以掌握。
除此之外,我们对上述代码进行一个简单的阐述:
l,r左右区间的取值。我们根据题目要求分析得知,要求解一个速度,这个速度是每次吃香蕉的速度,这个速度的最小值为 1, 最大值就是这一对香蕉里面最多的那个,速度介于[1, max(piles)]之间。分析这个也是求解二分问题的关键。check函数的作用是,求解速度为x的时候,吃完所有香蕉所需要的时间,其中吃一堆香蕉的时间可以分情况计算,向上取整就是这个速度吃完当前堆的香蕉所需要的时间。我们计算出这个时间,和给定的时间进行比较,如果说计算出来的时间不够吃完所有的香蕉,那么我们需要在右边区间搜索,反之也一样。
求根号 x 的值
可以使用二分法,解法一如下:
class Solution:
def mySqrt(self, x: int) -> int:
# 二分法
delta = 1e-5
l, r = 1, x
while l < r:
mid = (l + r) * 0.5
if abs(mid ** 2 - x) < delta:
return mid
elif mid ** 2 > x:
r = mid
else:
l = mid
return l解法二如下:
mid = (l + r) * 0.5
while True:
if mid ** 2 > x:
r = mid
else:
l = mid
last = mid
mid = (l + r) * 0.5
if abs(mid - last) < delta:
break
return mid解法一比解法二好很多,可以掌握一下!
如果是要求结果是整数,则使用以下解法:
class Solution:
def mySqrt(self, x: int) -> int:
# 二分法, 要求结果是取整的
l, r = 0, x
res = -1
while l <= r:
mid = (l + r) // 2
if mid ** 2 <= x:
res = mid
l = mid + 1
else:
r = mid - 1
return resLC719 找出第 K 小的数对距离
我们的解法如下:
class Solution:
def smallestDistancePair(self, nums: List[int], k: int) -> int:
# 这道题目为什么可以使用二分?
def count(mid: int) -> int:
# 这个函数求解,有多少对数字之间的距离小于等于 mid
# 已知 num, 并且 abs(num - x) <= mid, 由于我们枚举右边界去寻找左边界,则一定存在 num(右边界) > x
# 所以 num - x <= mid --> num - mid <= x, 我们需要找到 x 的位置, 范围是 0 ~ j
# 找到了左边界以后,所有满足的数字对的个数就是 j - i
res = 0
for j, num in enumerate(nums):
i = bisect_left(nums, num - mid, 0, j)
res += j - i
return res
# return bisect_left(range(nums[-1] - nums[0]), k, key=count)
nums.sort()
left, right = 0, max(nums) - min(nums)
while left <= right:
mid = left + (right - left) // 2
if count(mid) >= k:
right = mid - 1
else:
left = mid + 1
return left注释里面给出了一些思考的点,主要体现在以下方面:
- 对数组
nums进行排序 - 我们假设存在一个
mid, 这个mid是我们找到的两个数之间的距离的最大值,我们找到符合条件的数字x, 规定右边界,寻找左边界 - 根据一个右边界,找到所有的左边界,然后统计符合条件的数量,这个数量作为二分查找的条件
总结来说,这个题目的难点在于想到可以使用二分查找求解。
Merge PC(from work example)
下述代码是为了将相邻的 PC 进行合并,并产生新的 PC 和计数,比如说:
有一系列的 PC 列表,此时我们需要将连续的 PC 合并到一起,它们后面的技术也增加到合并的结果中。
def merge_continuous_addresses(address_list, count_list):
result = {}
i = 0
while i < len(address_list):
address = address_list[i]
count = count_list[i]
j = i + 1
current_sum = count
while j < len(address_list) and int(address_list[j], 16) == int(address, 16) + 4 * (j - i):
current_sum += count_list[j]
j += 1
result[address] = current_sum
i = j
return result而下面的这个例子则是用于查找:
def find_function_for_pc(functions, pc):
left = 0
right = len(functions) - 1
while left <= right:
mid = (left + right) // 2
start_address, function_size, function_name = functions[mid]
if int(start_address, 16) <= int(pc, 16) < int(start_address, 16) + int(function_size, 16):
return function_name
elif pc < start_address:
right = mid - 1
else:
left = mid + 1
return None已知我们有一个由 'FUNCTION_PC, FUNCTION_SIZE, FUNCTION_NAME' 组成的符号信息,目的是:给定一个 PC, 从符号信息中找到这个 PC 对应的函数名字。
在这种情况下,使用二分查找的效率就会高很多。
